HUBUNGAN DUA GARIS

Dua Garis Sejajar

---

Dua garis dikatakan memiliki hubungan sejajar jika gradiennya sama. Dua garis sejajar adalah dua garis yang jika sobat panjangkan berapapun tidak akan pernah berpotongan. Misal gradien garis 1 adalah m₁ dan gradien garis 2 adalah m₂ maka

m1 = m2


Contoh Soal
Jika sobat punya sebuah garis yang melewati titik (4,3) dan sejajar dengan garis 2x + y +7 = 0, coba sobat tentukan persamaan garis tersebut!
Jawab
dari persamaan garis 2x + y +7 = 0, buat memudahkan mencari gradien nilai c dianggap tidak ada
2x + y = 0
y = -2x –> didapat gradien garisnya = -2
nah untuk menentukan persamaan garis sobat pakai saja rumus y = mx + c. Masukkan titik (4,3)
y = mx + c
3 = (-2) 4 + c
3 = -8 + c
c = 11
jadi persamaan garis lurus sobat adalah y = -2x + 11 atau y + 2x – 11 = 0
kadang ada juga soal seperti ini, sebuah garis melewati titik (13,4) dan (15,1). Jika ada garis yang sejajar dengan garis tersebut melewati titik (6,4) Tentukan persamaan kedua garis tersebut!
Jawab.


Persamaan garis pertama kita selesaikan dengan rumus y = mx + c –> substitusi
titik (13,5) –> 5 = m₁13 + c
titik (16,1) –> 1 = m₁15 + c
———————————- -
4 = -2m₁
m₁ = -2
kita masukkan ke salah satu persamaan di atas untuk menemukan nilai c
5 = m₁13 + c
5 = (-2)13 + c
5 = -26 + c –> c = 31
jadi persamaan garis 1 adalah y = -2x + 31


Persamaan Garis kedua
m1 = m2 = -2
y = mx + c
4 = (-2)6 + c
4 = -12 + c
c = 16
jadi persamaan garis 2 –> y = -2x + 16

 

 

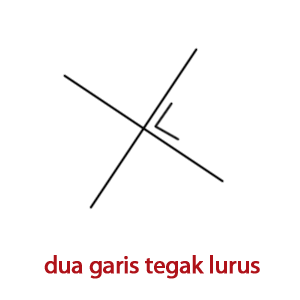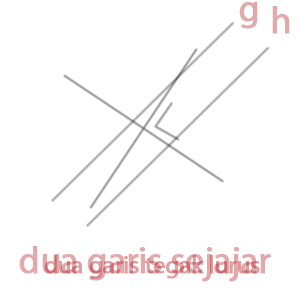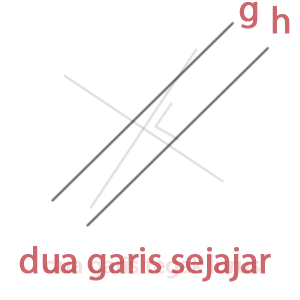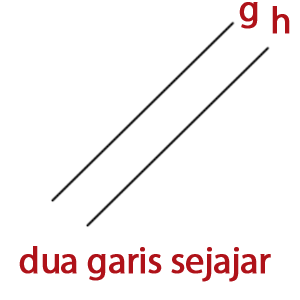
Dua Garis Tegak Lurus

---

Hubungan dua garis saling tegak lurus terjadi ketika perpotongan dua garis tersebut membentuk sudut 90^o. Jika garis a memiliki gradien m1 dan garis b memiliki gradien m2 maka rumus hubungan dua garis tersebut

m₁ x m₂ = -1
contoh soal
Tentukan hubungan 2 garis berikut g₁ :  3x + 4y = 5 dan g2 : 4x – 3y = 5
kita cari dulu gradien dari g1 dan g₂
3x + 4y = 5 (c tidak perlu kita anggap)
3x + 4y = 0
4y = -3x –> m₁ = -3/4
4x – 3y = 5 (c tidak kita anggap)
4x – 3y = 0
4x = 3y
y = 4/3 x –> m₂ = 4/3
m₁ x m₂ = -3/4 x 4/3 = -1 (jadi hubungan garis g1 dan g2 adalah tegak lurus)

 

 

Garis Saling Berpotongan

Dua garis saling berpotongan jika keduannya pernah melewati satu titik yang sama (hanya 1). Untuk menentukan titik potong tersebut kita bisa menggunakan  metode subtitusi maupun elminasi. Jika setelah disubtitusi dan dielminiasi bisa ketemu nilai x dan y maka kedua garis tersebut saling berpotongan. Buat lebih jelanya kita simak ilustrasi berikut.

Tentukan persamaan sebuah garis yang sejajar dengan garis 5x – y +12 = 0 dan melalui titik potong antara garis y = 2x – 5 dan y = 3x-7
Jawab
Karena sejajar maka gradien garis yang dicari sama dengan gradien garis  5x – y + 12 = 0, gradien didapat 5. Kemudian sobat cari titik potong antara garis y = 2x – 5 dan y = 3x-7, misal dengan substitusi
y = 2x – 5
y = 3x – 7
————— -
0 = -x + 2
x = 2, kita masukkan ke salah satu persamaan untuk mendapatkan niliai y
y = 2x – 5
y = 2(2) -5
y = -1, jadi kedua garis tersebut berpotongan di titik (2,-1)
persamaan garis
y = mx + c
-1 = 5.2 + c
-1 = 10 + c
c = -11
jadi persamaan garisnya adalah y = 5x -11

 

 

Dua Garis Berpotongan Membentuk Sudut α

---

Sebenarnya hubungan dua buah garis hanya ada 2 berpotongan dan tidak berpotongan. Berpotongan dibagi menjadi dua, tegak lurus (sudut 90^o) dan berpotongan tapi tidak tegak lurus (membentuk sudut α). Misal garis g dengan gradien mg berpotongan dengan garis h dengan gradien mh, dan terbentuk sudut α maka dirumuskan

             | m_g -m_h |
tan α = —————
             | 1 + m_g.m_h |

Yuk sobat simak contoh soal berikut, Tentukan besar sudut yang ibentuk oleh garis g : y = 3x  + 4 dan h : y = x + 4

            | m_g -m_h |
tan α = —————
             | 1 + m_g.m_h |
tan α =  | 3-1/ 1 + 3(1)  | = 1/2 dan arc tan 1/2 = 29,51^o. Jadi hubungan dua garis tersebut adalah berpotongan membentuk sudut lancip 29,51^o.