Untuk mempermudah pembahasan tentang gerakan, kita akan mulai
dengan benda-benda yang posisinya dapat digambarkan dengan menentukan
posisi satu titik. Benda semacam itu dinamakan partikel. Orang cendrung
membayangkan partikel sebagai benda yang sangat kecil, namun sebenarnya
tidak ada batas ukuran yang ditetapkan oleh kata partikel. Sebagai
contoh kadang-kadang lebih enak bila mengganggap bumi sebagai partikel
yang bergerak mengeliling matahari dalam lintasan yang menyerupai
lingkaran (tentunya jika dilihat dari planet atau galaksi lain yang jauh
bumi memang akan terlihat seperti sebuah titik kecil). Dalam kasus ini
kita tertarik untuk melihat lintasan pusat bumi mengelilingi matahari
sehingga ukuran dan rotasi bumi dapat kita abaikan.Dalam beberapa
persoalan astronomi bahkan keseluruhan tata surya dan galaksi dapat
dianggap sebagai sebuah partikel, Namun bila kita menganalisa rotasi
atau struktur internal dari bumi, maka kita tidak dapat lagi
memperlakukan bumi sebagai sebuah partikel tunggal. Tetapi pelajaran
kita tentang gerakan partikel tetap berguna, bahkan dalam kasus-kasus
ini sekalipun, karena benda apapun, tak peduli betapa rumitnya dapat
dianggap sebagai kumpulan atau sistem partikel.
1. Kelajuan, perpindahan dan kecepatan.
Kelajuan rata-rata partikel didefinisikan sebagai perbandingan jarak
total yang ditempuh terhadap waktu total yang dibutuhkan atau secara
matematis dapat ditulis :
Satuan SI kelajuan rata-rata adalah meter/sekon (m/s) dan satuan
lazin di US adalah feet/sekon (ft/s). satuan kelajuan sehari-hari di US
adalah mile/jam sedangkan dalam SI dikenal dengan km/jam.
Jika anda menempuh 200 km dalam 5 jam, maka kelajuan rata-rata anda
adalah : 200/50 = 40 km/jam. Kelajuan rata-rata tidak menceritakan
apa-apa tentang rincian perjalanan itu. Anda mungkin berkendaraan dengan
kelajuan tetap 40 km/jam selama 5 jam atau mungkin anda berkendaraan
cepat selama sebagian waktu dan lebih lambat selama sisa waktunya atau
mungkin anda telah berhenti untuk 1 jam dan kemudian berkendaraan dengan
kelajuan berubah-ubah selama 4 jam yang lainnya.
Sedangkan untuk konsep kecepatan sama dengan konsep kelajuan tetapi
berbeda karena kecepatan mencakup arah gerakan. Agar mengerti konsep
ini, terlebih dahulu akan diperkenalkan konsep perpindahan. Mari kita
buat sebuah sistem koordinat dengan memilih titik acuan pada sebuah
garis dengan titik asal O. untuk tiap titik lain pada garis itu kita
tetapkan sebuah bilangan x yang menunjukkan seberapa jauhnya titik itu
dari titik asal. Nilai x bergantung pada satuan (feet, meter atau
apapun) yang dipilih untuk mengukur jaraknya. Tanda x bergantung pada
posisi relatifnya terhadap titik asal O. kesepakatan yang biasanya kita
pilih adalah titik-titik di kanan titik asal diberi nilai positif dan
titik-titik dikirinya diberi nilai negatif.
Gambar 1 berikut ini menunjukkan sebuah titik yang berada pada posisi x1 pada saat t1 dan berada pada posisi x2 pada saat t2. Posisi partikel dari titik x2 – x1
disebut perpindahan partikel. Biasanya digunakan huruf Yunani delta (∆)
untuk menyatakan perubahan kuantitas, jadi perubahan x dapat ditulis
menjadi ∆x atau secara matematis dapat ditulis :
Gambar 1 perpindahan partikel dari x1 ke x2
Kecepatan adalah laju perubahan posisi. Kecepatan rata-rata partikel
didefinisikan sebagai perbandingan antara perpindahan (∆x) dengan selang
waktu (∆t = t2 – t1). Atau dapat ditulis dalam bentuk rumus :
Perhatikan bahwa perpindahan dan kecepatan rata-rata dapat bernilai positif atau negatif, bergantung pada nilai x2 dan x1.
Sesuai dengan perjanjian nilai positif menyatakan partikel bergerak ke
kanan dan nilai negatif menyatakan partikel bergerak ke kiri.
Perhatikan gambar 2 berikut ini. Pada gambar ini terlihat sebuah
lintasan partikel yang berbentuk kurva dalam bidang koordinat x terhadap
t, dimana x menyatakan jarak dan t menyatakan waktu. Tiap titik pada
kurva mempunyai nilai x, yang merupakan lokasi partikel pada saat
tertentu, dan sebuah nilai t, yang merupakan saat partikel berada
dilokasi tersebut. Pada grafik kita gambar garis lurus antara posisi
yang dinamai P1 dan posisi yang dinamai P2, perpindahan ∆x = x2 – x1 dalam selang waktu ∆t = t2 – t1 . garis lurus yang menghubungkan P1 dan P2
adalah sebuah sisi miring segitiga yang memiliki sisi tegak lurus ∆x
dan sisi datar ∆t. Rasio ∆x/∆t adalah kemiringan (gradien) garis lurus
ini. Dalam istilah goemetri, kemiringan ini merupakan ukuran kecuraman
garis lurus pada grafik. Untuk selang waktu tertentu ∆t, makin curam
garisnya, makin besar nilai ∆x/∆t. Karena kemiringan garis ini adalah
kecepatan rata-rata untuk selang waktu ∆t, maka kita mempunyai tampilan
bentuk geometrik untuk kecepatan rata-rata.
Gambar 2 grafik x terhadap
2. Kecepatan sesaat
Kecepatan sesaat pada saat tertentu adalah kemiringan garis lurus
yang menyinggung kurva x terhadap t pada saat itu. Gambar 3 adalah kurva
x terhadap t yang sama seperti pada gambar 2 yang menunjukkan ururtan
selang waktu ∆t, ∆t1, ∆t2, ∆t3,….. yang
masing-masing lebih kecil daripada selang sebelumnnya. Untuk tiap
selang waktu ∆t, kecepatan rata-rata adalah kemiringan garis lurus yang
sesuai untuk selang itu. Gambar menunjukkan bahwa, jika selang waktu
menjadi lebih kecil, garis lurusnya menjadi semakin curam, tetapi garis
tersebut tak pernah lebih miring dari pada garis singgung pada kurva t1. Kemiringan garis singgung ini kita definisikan sebagai kecepatan sesaat pada t1.
Gambar 3 grafik x versus t dari gambar 2
Penting disadari bahwa perpindahan ∆x bergantung pada selang waktu
∆t. Ketika ∆t mendekati nol, demikian juga ∆x (seperti dapat dilihat
dari gambar 3), rasio ∆x/∆t mendekati kemiringan garis yang menyinggung
pada kurva. Karena kemiringan garis singgung adalah limit rasio ∆x/∆t
jika t mendekati nol. Kita dapat menyatakan kembali definisi kita
sebagai berikut :
Kecepatan sesaat adalah limit rasio ∆x/∆t jika ∆t mendekati nol atau secara matematis dapat ditulis :
Limit ini dinamakan turunan x terhadap t dalam notasi kalkulus ditulis :
Kemiringan ini dapat positif (x bertambah besar) atau dapat juga
negatif (x bertambah kecil), dengan demikian dalam gerak satu dimensi ,
kecepatan sesaat dapat bernilai positif maupun negatif. Besarnya
kecepatan sesaat disebut kelajuan sesaat.
3. Percepatan
Bila kecepatan sesaat sebuah partikel berubah seiring dengan
berubahnya waktu, maka partikel dikatakan dipercepat. Percepatan
rata-rata untuk suatu selang waktu tertentu ∆t = t2 – t1 didefinisikan sebagai rasio ∆v/∆t dengan ∆v = v2 – v1 adalah perubahan kecepatan sesaat untuk selang waktu tersebut.
Dimensi percepatan adalah panjang dibagi (waktu) 2. Satuan yang umum adalah meter per sekon kwadrat atau ditulis m/s2. Artinya bila suatu benda dipercepat dengan percepatan 10 m/s2,
maka tiap detik , kecepatan benda tersebut bertambah sebesar 10 m/s.
misalnya pada saat t=0; v = 0 maka untuk detik pertama (t=1) maka
kecepatan benda menjadi 10 m/s, untuk detik kedua (t=2) kecepatan benda
menjadi 20 m/s dan seterusnya.
4. Percepatan sesaat
Percepatan sesaat adalah limit (rasio ∆v/∆t) dengan ∆t mendekati nol.
Jika kita gambar grafik kecepatan terhadap waktu , percepatan sesaat
pada saat t didefinisikan sebagai kemiringan garis yang menyinggung
kurva pada saat itu
Jadi percepatan adalah turunan kecepatan terhadap waktu. Notasi
kalkulus untuk turunan ini adalah dv/dt. Karena kecepatan adalah turunan
posisi x terhadap waktu t, percepatan adalah turunan kedua x terhadap
waktu t, yang biasanya ditulis d2x/dt2. Kita dapat melihat alasan notasi semacam ini dengan menulis percepatan sebagai dv/dt dan mengganti v dengan dx/dt:
Jika kecepatan konstan maka percepatan akan sama dengan nol atau ∆v =
0 untuk seluruh selang waktu. Dalam hal ini kemiringan kurva x terhadap
t yang bersangkutan tidak berubah. Secara matematik hubungan,
percepatan, kecepatan, jarak dan waktu dapat dijabarkan sebagai berikut :
Perubahan jarak terhadap waktu adalah kecepatan :
Perubahan kecepatan terhadap waktu adalah percepatan :
Sumber :
1. Tipler; Fisika untuk sains dan teknik jilid 1, Erlangga
2. Halliday Resnick, Fiska jilid 1, Erlangga
Gerak dengan percepatan konstan
Di sekitar kita banyak dijumpai gerak dengan percepatan konstan,
misalnya gerak jatuh bebas sebuah benda. Pada saat benda dijatuhkan dari
ketinggian tertentu, maka benda tersebut akan mengalami percepatan yang
besarnya tetap yaitu sebesar percepatan gravitasi bumi (9,81 m/s2 atau 32 ft/s2).
Gerak dengan percepatan konstan akan memiliki kemiringan kurva v
terhadap t yang konstan artinya kecepatan berubah secara linier terhadap
waktu. Jika nilai kecepatan awal adalah v0 pada saat t = 0, nilai v pada saat t berikutnya diberikan oleh :
Jika partikel memulai gerakan di x0 pada saat t =0 dan posisinya adalah x pada saat t, perpindahan ∆x = x– x0 diberikan oleh :
Kecepatan rata-rata dapat dihitung dengan persamaan :
Jadi perpindahan adalah :
Bila v = v0 + at maka kita mendapatkan persamaan perpindahan adalah :
Bila diketahui t = (v – v0)/a maka didapat :
Jika tiap ruas dikalikan dengan a dan tiap sukunya dijabarkan, maka akan didapat :
Integrasi
Bagaimana caranya kita mendapatkan fungsi kecepatan dan percepatan
dari suatu fungsi posisi yang diketahui lewat diferensiasi. Persoalan
kebalikannya adalah mendapatkan fungsi posisi x bila diketahui kecepatan
v atau percepatan a. Untuk melakukan hal ini kita menggunakan sebuah
prosedur yang dinamakan integrasi. Contoh mendapatkan nilai kecepatan
dan posisi dari percepatan yang diberikan. Jika kita mengetahui
percepatan itu sebagai fungsi waktu, kita dapat menemukan kecepatan
dengan mencari fungsi v(t) yang turunannya adalah percepatan. Sebagai
contoh jika percepatan konstan
Maka kecepatan adalah fungsi waktu yang bila dideferensiasikan sama dengan konstanta ini. Fungsi semacam ini adalah :
Namun persamaan ini bukanlah persamaan yang paling umum untuk v yang
akan memenuhi hubungan dv/dt = a. Secara khusus kita dapat menambahkan
sembarangan konstanta pada at tanpa mengubah nilai turunannya terhadap
waktu. Dengan menamakan konstanta ini vo, kita mendapatkan :
Konstanta v0 adalah kecepatan awal. Fungsi posisi x adalah fungsi yang turunannya adalah kecepatan:
Kita dapat mengolah tiap suku secara terpisah, fungsi yang turunannya terhadap waktu adalah konstanta v0 adalah v0t ditambah dengan sebuah konstanta sembarang. Sedangkan fungsi yang turunannya at adalah 1/2at2
ditambah dengan sebuah konstanta sembarang. Dengan menggabungkan hasil
integrasi ini dan menambahkan sebuah konstanta gabungan sembarang x0 maka kita mendapatkan :
Bilamana kita mendapatkan sebuah fungsi dari turunannya maka kita
juga harus menyertakan sebuah konstanta sembarang dalam fungsi umumnya.
Karena kita harus melakukan 2 kali proses integrasi untuk mendapat x(t)
dari fungsi a(t) maka muncul 2 buah konstanta. Konstanta-konstanta ini
biasanya ditentukan dari kecepatan dan posisi pada suatu saat tertentu,
yang biasanya dipilih pada saat t = 0. Oleh sebab itu kedua konstanta
itu disebut kondisi awal.






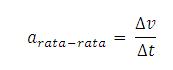
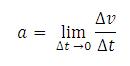
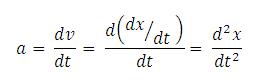
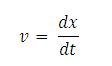
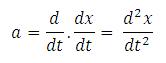
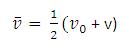



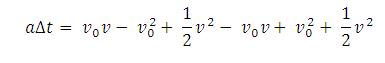


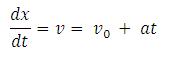
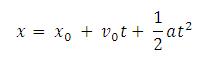
No comments:
Post a Comment