Torsi

Sebuah partikel yang terletak pada posisi
r relatif terhadap sumbu rotasinya. Ketika ada gaya
F yang bekerja pada partikel, hanya komponen tegak lurus
F⊥ yang akan menghasilkan torsi. Torsi
τ =
r ×
F ini mempunyai besar
τ = |
r| |
F⊥| = |
r| |
F| sin
θ yang arahnya keluar bidang kertas.
Torsi atau
momen gaya adalah hasil kali antara gaya F dan lengan momennya. Torsi dilambangkan dengan lambang

.

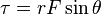
Satuan dari torsi adalah
Nm (Newton meter).
Momen inersia
Momen inersia adalah hasil kali partikel massa dengan kuadrat jarak tegak lurus partikel dari titik poros.

Satuan dari momen inersia adalah
kg m² (Kilogram meter kuadrat).
Besaran momen inersia dari beberapa benda.
| Benda |
Poros |
Gambar |
Momen inersia |
| Batang silinder |
Poros melalui pusat |
 |
 |
| Batang silinder |
poros melalui ujung |
 |
 |
| Silinder berongga |
Melalui sumbu |
 |
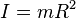 |
| Silinder pejal |
Melalui sumbu |
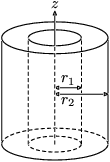 |
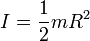 |
| Silinder pejal |
Melintang sumbu |
 |
 |
| Bola pejal |
Melalui diameter |
 |
 |
| Bola pejal |
Melalui salahsatu garis singgung |
 |
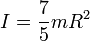 |
| Bola berongga |
Melalui diameter |
 |
 |
Hubungan antara torsi dengan momen inersia
Hukum II Newton tentang rotasi
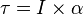
Keterangan:
- I : momen inersia (kg m²)
- α : percepatan sudut (rad/s²)
 : torsi (Nm)
: torsi (Nm)
 .
.
 : torsi (Nm)
: torsi (Nm)

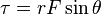





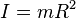

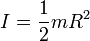




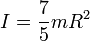


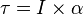
No comments:
Post a Comment