Di dalam kapasitor terdiri dari 2 buah terminal atau sering disebut lempeng konduktor dan bahan dielektrik yang disisipkan di antara kedua lempeng konduktor. Dielektrik adalah bahan isolator yang dapat digunakan untuk meningkatkan kapasitas sebuah kapasitor. Kapasitor sederhana dapat dengan mudah dibuat dengan menggunakan 2 buah lempengan aluminium dan selembar kertas.
Untuk membuat kapasitor sederhana ini kita hanya membutuhkan 2 lempengan aluminium dengan tebal 1 mm, 1 lembar kertas, sedikit kertas untuk isolator, dan 2 buah penjepit kertas.
Secara teori, bahan dielektrik adalah sejenis isolator. Banyak bahan yang dapat digunakan sebagai bahan dielektrik sebuah kapasitor antara lain : keramik, mika, kaca, kertas, udara, serat selulosa, porselein, mylar, teflon dan bahan kimia cair. Penggunaan bahan-bahan dielektrik ini disesuaikan dengan penggunaan kapasitor itu sendiri. Berikut adalah contoh penggunaan kapasitor yang disesuaikan dengan bahan dielektriknya :
- Bahan dielektrik udara atau lebih dikenal dengan variabel kapasitor, umumnya digunakan untuk men-turning frekuensi radio.
- Kapasitor mylar dengan bahan dielektrik mylar umum digunakan pada rangkaian clock frekuensi, alarm atau counter.
- Gelas atau kaca untuk digunakan pada kapasitor yang bekerja pada tegangan tinggi.
- Kapasitor keramik banyak digunakan pada frekuensi tinggi. Seperti pada rangkaian pemancar dan antena, mesin sinar X dan mesin MRI.
- Kapasitor elektrolit dengan bahan dielektrika dari bahan kimia cair, umum digunakan pada frekuensi rendah dan rangkaian daya. Kapasitor elektrolit ini umumnya memiliki kapasitas yang besar-besar.
- Super kapasitor adalah kapasitor dengan muatan yang cukup besar bekerja pada tegangan rendah dan memiliki waktu pengisian yang sangat singkat. Super kapasitor umum digunakan pada rangkaian daya listrik dan mobil – mobil tenaga listrik.
Sebuah kapasitor dalam kondisi tidak diisi muatan listrik, maka pada kedua lempeng konduktornya tidak akan ada muatan listrik. Selama proses pengisian kapasitor, sebuah muatan listrik dipindahkan dari satu konduktor ke konduktor lainnya dan memberikan muatan positif pada salah satu lempeng konduktor dan muatan negatif pada lempeng konduktor lainnya. Contoh sederhana sebuah kapasitor dapat dibuat dari 2 lempengan konduktor dengan luas permukaan yang sama (A), yang dipasangkan paralel satu dengan lainnya dan terpisah pada jarak d seperti pada gambar berikut ini.

Gambar 3 ilustrasi sebuah kapasitor sederhana
Melalui percobaan banyaknya muatan (Q) yang disimpan dalam sebuah
kapasitor besarnya linier dan proporsioal terhadap beda tegangan pada
kedua lempeng konduktor kapasitor atau secara matematis dapat ditulis :
Dimana Q : muatan listrik (satuan Coulomb ( C ) )
C : kapasitas kapasitor (satuan Farrad (F))
Menghitung Kapasitas Kapasitor
Bila ada 2 buah pelat konduktor dengan luas permukaan yang sama yaitu A yang dipisahkan pada jarak d, kemudian lempeng konduktor bagian atas diberi muatan +Q dan lempeng konduktor bagian bawah diberi muatan –Q, maka medan muatan pada 2 buah lempeng konduktor tersebut dapat digambarkan sebagai berikut
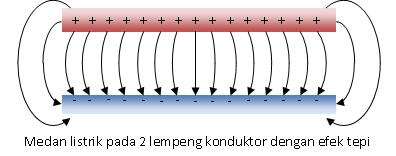
Untuk menghitung kapasitas kapasitor (C), pertama-tama kita harus mengetahui medan listrik antara kedua lempeng konduktor. Sebenarnya sebuah kapasitor memiliki ukuran lempeng konduktor yang terbatas panjangnya. Maka garis medan listrik pada ujung pelat tidaklah berupa garis lurus, tetapi berbentuk kurva lengkung yang disebut efek tepi. Medan listrik pada ujung lempeng konduktor ini tidak seragam, namun untuk memudahkan menghitung kapasitas kapasitor, kita akan mengabaikan efek ujung ini.
Dengan asumsi lempeng konduktor tidak terbatas panjangnya dan sistem mempunyai bentuk yang simetri, maka kita dapat menghitung medan listrik di sembarang tempat dengan menggunakan persamaan hukum Gauss didapat:
Dimana A’ : luas penampang Gaussian dapat digambarkan sebagai berikut.
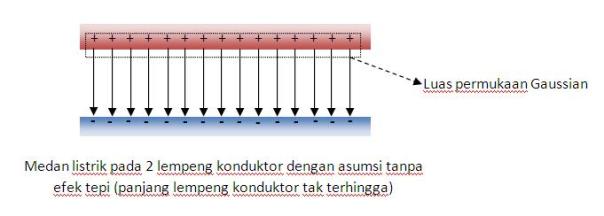
Beda potensial listrik antara 2 lempeng konduktor adalah :
Dari persamaan awal (
Dimana :
d : jarak pisah antara 2 lempeng konduktor (m)
A : luas permukaan lempeng konduktor yang berhadapan (m2)
Q : besar muatan listrik ( C )
” sedikit catatan : “
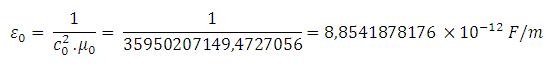
c0 : kecepatan suara
µ0 : permeabilitas ruang hampa
Untuk kapasitor sederhana yang terdiri 2 lempeng konduktor sejajar, kapasitas kapasitor sangat ditentukan oleh dimensi kapasitor.
” uraian di atas menunjukan cara menghitung kapasitas sebuah kapasitor berbentuk lempengan dengan luas permukaan dan jarak diketahui, terus bagaimana jika kapasitor tersebut berbentuk seperti sebuah tabung ?, nah berikut uraiannya. “
Menghitung Kapasitas Kapasitor tipe Silinder.
Sebuah konduktor silinder dengan jari-jari a diselimuti oleh sebuah tabung dengan jari-jari bagian dalam b seperti pada gambar berikut ini.
Panjang kapasitor adalah L dan panjang L jauh lebih besar dibandingkan jarak b – a. efek tepi diabaikan untuk memudahkan perhitungan. Inti bagian dalam tabung kapasitor diberi muatan +Q dan selimut tabung diberi muatan listrik –Q, maka hukum Gauss untuk kapasitor silinder dapat ditulis :
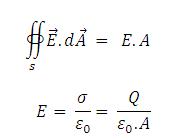 A adalah luas permukaan tabung yang besarnya A = 2πrL dan
A adalah luas permukaan tabung yang besarnya A = 2πrL dan Beda potensial antara inti silinder dengan selimut tabung adalah :
Maka kapasitas kapasitor didapat :
Dapat dilihat dari persamaan kapasitor silinder, bahwa kapasitas sebuah kapasitor berbentuk silinder sangat ditentukan oleh dimensi kapasitor tersebut.
” Fisika memang unik dan menarik, setelah kita dapat menghitung kapasitor berbentuk tabung, muncul lagi bahasan yang lainnya, bagaimana kapasitas sebuah kapasitor berbentuk bola. salah satu model ini adalah pada bola logam yang terdapat pada generator van de graff. Apa generator van de graff?…..(what hari gini gak kenal generator van de graff???????? oh my God) lihat gambar berikut :
Bola logam besar pada generator Van De
Graff adalah sebuah kapasitor besar. Nah sekarang mari kita lihat
bagaimana cara menghitung kapasitasnya>
lanjut……………………. “
Menghitung kapasitas kapasitor tipe bolaPada bagian ini kita akan menghitung kapasitas sebuah kapasitor yang berbentuk bola. Bila ada sebuah kapasitor yang terdiri dari 2 buah bola yang disusun paralel dengan bola yang kecil di bagian dalam dan bola yang lebih besar di bagian luar. Bola yang dibagian dalam diberi potensial listrik positif dan bola bagian luar di beri potensial negative seperti pada gambar berikut ini.

Gambar 6 ilustrasi model kapasitor berbentuk bola
Pada bola yang diberi potensial listrik positif akan ada muatan
listrik positif dan pada bola yang diberi potensial listrik negaitf akan
ada muatan listrik negatif. Jari-jari bola kecil adalah a dan jari-jari
bola besar adalah b. sedangkan r adalah jari-jari luas bidang Gaussian,
maka medan listrik pada daerah a < r < b dapat dihitung :Beda potensial antara 2 konduktor yaitu bola dalam dan bola luar dapat dihitung :
Maka kapasitas kapasitor tipe bola dapat dihitung :
Sekali lagi terlihat bahwa kapasitas kapasitor sangat ditentukan oleh dimensi kapasitor ( a dan b).
Bila konduktor b memiliki ukuran yang “tak terhingga” atau secara matematis ditulis

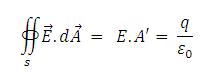
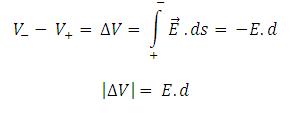

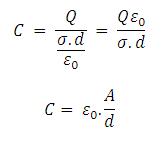

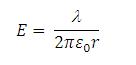
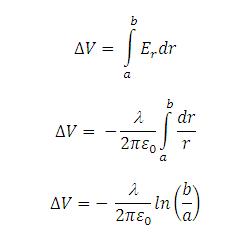



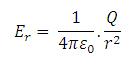
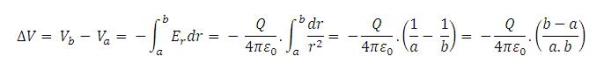
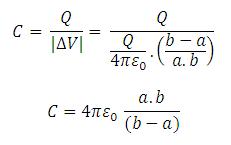

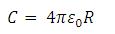
No comments:
Post a Comment